1. Định luật bảo toàn động lượng:
Tag: gia sư lý tại nhà
- Điều kiện áp dụng: HỆ KÍN- Xác định động lương của hệ trước và sau tương tác.-Hay:
- Vẽ hình các. Các em cần chú ý:
- Chuyển về biểu thức đại số:Cách 1: Chọn hệ trục Ox, Oy thích hợp và dùng phương pháp hình chiếu.Cách 2: sử dụng quy tắc hình bình hành. Thường cách này được sử dụng khi các vectơtạo thành các tam giác vuông, tam giác đều, tam giác cân.
2. Ví dụ minh họa:
Một viên đạn khối lượng 2 kg đang bay thẳng đứng lên cao với vận tốc 250 m/s thì nổ thành 2 mảnh có khối lượng bằng nhau. Biết mảnh 1 bay với vận tốc 250 m/s theo phương ngang. Hỏi mảnh thứ hai bay theo phương nào với vận tốc bằng bao nhiêu?
Giải:
- Trước tiên, các em sẽ nhận thấy hệ này là hệ kín vì:
- Trước khi nổ, ta có: 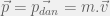
- Sau khi nổ, viên đạn tách ra thành 2 mảnh nên: 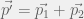 với
với 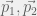 lần lượt là động lượng của mảnh 1 và 2.
lần lượt là động lượng của mảnh 1 và 2.
- Theo định luật bảo toàn động lượng, các em sẽ có: 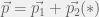
Sau
khi phân tích các yếu tố xong,theo yêu cầu của đề bài, các em phải xác
định phương và vận tốc của mảnh 2. Nghĩa là: cần phải xác định được 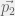 .
.
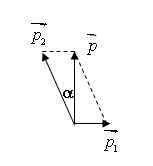
- Muốn vậy, ta tiến hành vẽ hình bình hành để xác định 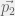
- Đầu tiên, vẽ vectơ 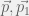 đã biết hướng.
đã biết hướng.
- Dùng quy tắc hình bình hành vẽ vectơ 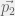
- Chuyển về biểu thức đại số:
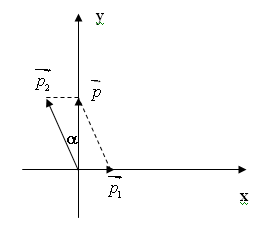
Chiếu (*) xuống 2 trục Ox, Oy. Ta có:
Lấy (1) chia cho (2) ta có: 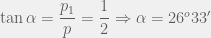
Suy ra: 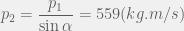
Do đó: 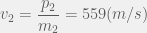
Cách 2:
Theo định lý Pitago ta có:
Suy ra: 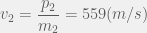
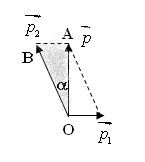
Ta lại có, Trong tam giác vuông OAB:
Vậy sau khi nổ, mảnh 2 bay theo hướng chếch lên, hợp với phương thẳng đứng 1 góc 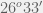 , với vận tốc 559 m/s
, với vận tốc 559 m/s
Nhận xét:
- Với bài toán này, thì ta sử dụng cách 2 sẽ cho kết quả nhanh hơn.
3. Bài tập áp dụng:
Bài 1: Giải lại ví dụ trên nếu mảnh 1 bay theo phương lệch 1 góc 60 so với đường thẳng đứng.
Đ/S: 433 m/s, hợp với phương thẳng đứng góc 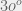
Bài 2: Viên đạn khối lượng m = 0,8 kg đang bay ngang với vận tốc 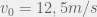 thì vỡ làm hai mảnh. Mảnh 1 có khối lượng
thì vỡ làm hai mảnh. Mảnh 1 có khối lượng 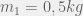 , ngay sau khi vỡ rơi thẳng đứng xuống với vận tốc
, ngay sau khi vỡ rơi thẳng đứng xuống với vận tốc 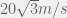 . Tìm độ lớn và hướng vận tốc của mảnh 2 ngay sau khi vỡ.
. Tìm độ lớn và hướng vận tốc của mảnh 2 ngay sau khi vỡ.
Đ/s: 66,7 m/s, hợp với phương ngang 1 góc 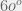
Bài 3: Viên đạn khối lượng m = 0,8 kg đang bay ngang với vận tốc 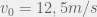 thì vỡ làm hai mảnh ở độ cao H = 20 m.
thì vỡ làm hai mảnh ở độ cao H = 20 m.
Mảnh 1 có khối lượng 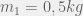 , ngay sau khi vỡ rơi thẳng đứng xuống đứng và khi sắp chạm đất có vận tốc
, ngay sau khi vỡ rơi thẳng đứng xuống đứng và khi sắp chạm đất có vận tốc 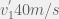 . Tìm độ lớn và hướng vận tốc của mảnh 2 ngay sau khi vỡ. Bỏ qua lực cản không khí.
. Tìm độ lớn và hướng vận tốc của mảnh 2 ngay sau khi vỡ. Bỏ qua lực cản không khí.
———————————————————————————————————————————————-
Nguyễn Hoàng Trúc (Mrs)
Thạc sĩ Quang học.
Giáo viên bộ môn Vật Lý.
Trường Trung học thực hành – ĐH Sư Phạm Tp. Hồ Chí Minh

Không có nhận xét nào:
Đăng nhận xét